I’ve been seeing videos of Terrence Howard, the original War Machine in the first Iron Man movie alongside Robert Downey Jr., pop up on my social media over the last few weeks, particularly a video where he discovers an “unnatural loop” within mathematics:
- Take the square root of 2.
- Cube it.
- Divide it by 2.
- You’re back at the start: the square root of 2.

Howard claims that this loop is “unnatural” and exposes the brokenness of the square root of two itself, and therefore, the entire system of mathematics upon which it’s built. As he puts it, “we’ve been living in this fostered lie for so long.” Howard uses this, and other examples, as proclaimed evidence that mathematics is, and always has been, fundamentally misguided, and has been working on his own framework which is infamous for its claim that 1⋅1=2.
Based on the few videos I’ve seen, my impression is that Terrence Howard is in disbelief from incredulity; the result, to him, seems counterintuitive and unexpected, so he chooses to believe it is invalid accordingly. I don’t know enough about Terrence Howard to conclusively state that my impression is correct. If it is, this isn’t the right way to learn about the world, to make discoveries, or to make claims, certainly not so bold as to say that the foundation of mathematics is crumbling beneath us.
Instead, he should ask himself why does this happen? That was the question I asked myself the first time I saw him describe this. In this post, I’m going to briefly outline what the “loop” is, why it makes sense, and generalize it to gain a deeper understanding of the concepts at play.
Analyzing the Loop
The operation described above is modeled by the equation below:
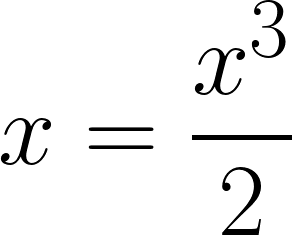
In other words, if you raise x to the third power and divide that by two, the result is that original value of x. From Howard’s original statement, we know that the square root of two satisfies this equation, but let’s work through the steps of solving this to see if any other answers also satisfy this.

We see that there are two answers, the square root of two, and its negative. This shows that for Howard’s original procedure of cubing, then dividing by two, the square roots of two, both positive and negative, are the only numbers that satisfy the model. In other words, they’re the only numbers that “loop” in this way. In this specific case, the operation of dividing by two is equivalent to the operation of taking the cube root, and in the general case, taking the cube root of a cubed number results in that original number, so in either case, no loop exists.
While Howard’s claim that this specific “loop” doesn’t exist anywhere else is true for this specific model, there are infinitely many similar “loops” that exist. In the section below, we’ll generalize the model to gain a deeper understanding of how it works and what similar models exist.
Deeper Insights into the Loop
Let’s generalize the model above by replacing 3 with y and 2 with y-1:
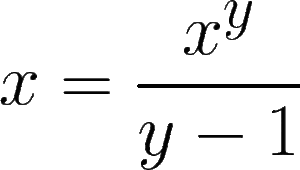
Now, we can provide any value for y. The question is, do any values of x exist where y is not equal to 3? In other words, does this “loop” exist anywhere else in the same form?
This is a tricky equation to work with because involves two variables, one of which is raised to the power of the other. Instead of trying to isolate y directly, let’s work from a conjecture. When I originally tackled this problem, I observed this relationship between y and x from the original model in the previous section:
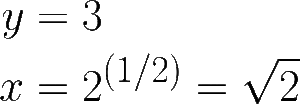
The value x above can be substituted for y-1 to the root of y-1., analogous to 2 to the root of 2. My conjecture is that for all y, the following holds for x:
![]()
This equation isolates x in terms of y, and if true, would prove that there are infinitely many such “loops” of this form.
Let’s try to prove it by substituting it back into the generalized model above:
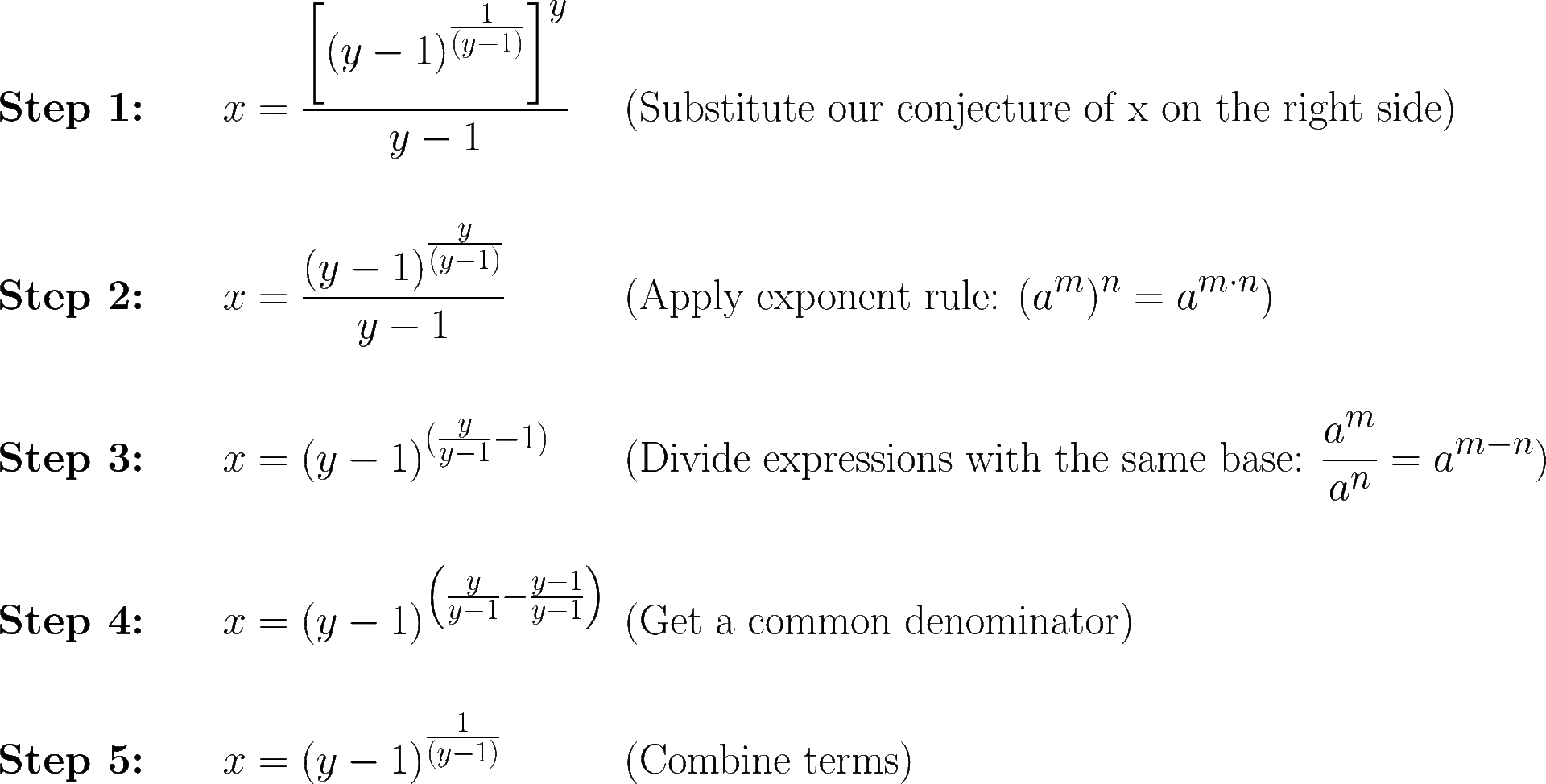
In the first step above, we substituted the occurrence of x on the right side with the assignment made in the conjecture. Then, we reduced it until the last step, where we found that
we’ve derived the statement we’ve made in the conjecture, thereby proving the conjecture true. This means that you can pick any value of y, find it’s corresponding x value, and thereby create your own “loop.” For example, if we say that y is 4, then x is the cube root of 3, and we have a loop:
- Take the cube root of three, roughly 1.4422…
- Raise it to the fourth power, which is roughly 4.3627…
- Divide it by three, which brings you back to 1.4422…
Let’s make one with 5,627:
- The 5,626th root of 5,626 is roughly 1.0015…
- Raise it to the 5,627 power, which is roughly: 5634.64…
- Divide it by 5626, which brings you back to 1.0015…
With that, we have infinitely many solutions for x and y, which means we have infinitely many “loops.” As a note, you can further generalize to replace (y-1) with (y-z) and generate infinitely many more solutions.
Conclusion
As a rule, I try to be as open and inquisitive as possible, trying not to take anything for granted and ready to entertain any idea or concept, knowing that the concept will either stand up on its own merit, fall flat, or remain indeterminate, so long as I properly consider it and admit when I don’t have enough knowledge or understanding to carry that consideration through to the end. This is the best, and perhaps only, real defense against biases of all kinds: conscious preferences for a particular set of outcomes, unconscious biases based on held convictions and beliefs, unconscious biases based on previous observations, and a myriad of others. Without this defense, anyone and everyone will find themselves susceptible to believing unproven ideas, false ideologies, biased individuals, or any number of similar risks, and the dangers associated with them. With this defense, you can not only help protect yourself against the bad, but you also put yourself on solid footing on the road toward making novel insights, new discoveries, and ultimately toward a better self.