How to Update Your Beliefs Mathematically

A few months ago, I read Steven Pinker’s book “Rationality: What It Is, Why It Seems Scarce, Why It Matters.” This book gives a bird’s eye view of the landscape of rationality, dedicating one chapter to each facet of reasoning, including formal logic, game theory, and working with beliefs and evidence. Regarding the latter, Pinker discusses an interesting form of reasoning called Bayesian reasoning that focuses on updating beliefs. The likelihood that a belief is accurate changes based on new evidence and this can be calculated mathematically with enough information.

The key component of Bayesian reasoning is Bayes’ Theorem. This is a theorem that outlines how to update your belief, or hypothesis, that something will happen given your prior knowledge of the event and surrounding circumstances. The formal definition of this theorem is:

The probability that some hypothesis is true, given that some past event has taken place, equals the probability that the hypothesis is true independent of that event, multiplied by the probability that event has taken place given the probability of the hypothesis, scaled by the probability that event would take place independent of your hypothesis.

That definition is undoubtedly hard to read, so let’s use an example to show how it works.

Imagine that you take an at-home COVID-19 test with a 95% accuracy rate. It gives a false negative 5% of the time and a false positive 5% of the time. If you test positive, what are the chances you have Covid 19?

Most people would answer something around 95%, including doctors who administer such tests. That answer is highly incorrect because it does not factor in the base rate, i.e. what percentage of the population does have covid (or does not). To demonstrate, let’s say that roughly 12% of the population has Covid (this was roughly the percentage in late 2020). Let’s take our definition of Bayes’ theorem above and put some numbers in. The hypothesis is that you have Covid and the event is that you’ve tested positive for Covid:

1. Probability that your hypothesis is true prior to the event taking place: 12%, since 12% of the population has Covid (in this example).
2. Probability of that event taking place given the hypothesis is true: 95%, since the Covid test has a 95% accuracy rate.
3. Probability that the event would take place independent of the hypothesis:
   • If you do actually have covid: 95% * 12% (true positive rate multiplied by the percentage of the population that has Covid).
   • If you don’t have covid: 5% * 88% (false positive rate multiplied by the percentage of the population that does not have Covid).
   • Total: 95%*12%+5%*88%=15.8%

The probability that you have COVID-19, given that you’ve tested positive, according to the definition above, is 72.15%. This number would be much lower if the prevalence of COVID-19 were more negligible, but it doesn’t provide the same guarantee that you have COVID-19 as a number such as 95% seems to. Imagine if this were a test for a deadlier but less common disease; the percentage would be much lower.

Now, let’s say you want a second opinion, so take a different Covid test with a 7% false positive and 7% false negative rate. You also test positive on this one. You want to ensure that you factor in the previous test’s results. Here are the new calculations where the event is your second COVID test:

1. Hypothesis is true prior to the event taking place: 72.15% based on the results of your previous test.
2. Probability of the event taking place given the hypothesis is true: 93%, since the Covid test has a 93% accuracy rate.
3. Probability that the event would take place independent of the hypothesis: this calculation is a bit different since we are factoring in our previous test result.
   • If you do actually have covid: 93% * 72.15% (true positive rate multiplied by the probability that you have covid from the previous test).
   • If you don’t have covid: 7% * 17.85% (false positive rate multiplied by the percentage of the population that does not have Covid).
   • Total: 0.93*0.7215+0.05*0.1785=68%

Now, the probability is 98.7%. With two different tests, which both indicate positive, there is a very high probability that you have Covid.

In this scenario, we formed a hypothesis, determine the probability that it is correct, then updated our beliefs accordingly. In the second round of calculations, we used that updated belief to determine a new probability, then updated our beliefs again accordingly. In general, it is important to update your beliefs with new evidence as it becomes available, and Bayesian reasoning incorporates this mathematically. In your day-to-day, when you’re making decisions, you probably won’t have numeric probabilities to work with, but you can still use the underlying concepts to help you make more logical choices.

---

Just out of curiosity, what would the percentage of the population that has Covid need to be for the first test, which has a 95% accuracy, to be right 95% of the time after the first test? Let’s use the mathematical representation of Bayes’ Theorem to answer this:

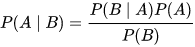
• In this example, A is the hypothesis that I have Covid and B is the event of me testing positive for Covid.
• P(A | B) is the probability that the hypothesis A is true given that event B has taken place. It reads as “probability of A given B”.
• P(A) is the probability that the hypothesis is true prior to the event taking place.
• P(B | A) is the probability of the event taking place given that the hypothesis is true.
• P(B) is the probability that the event would take place (regardless of whether or not the hypothesis is true).

To answer the question above, we can use the information we already have to fill in the blanks:

• P(A | B) = 95% (we want to find the percentage of the population which makes the value 95%, so we can plug it in directly).
• P(B | A) = 95% (that is the accuracy of our test)

We can formulate as: 0.95=0.95*P(A)/P(B). Before, we were implicitly calculating P(B); now, we’ll explicitly define: P(B)=P(B | A)*P(A)+P(B | not A)*P(not A), which in this context means the probability that you have a true positive if you have Covid or a false positive if you don’t. We can rewrite our formula as: 0.95=0.95*P(A)/(0.95*P(A)+0.05*P(not A). Since P(A) is a percentage of population, we can write it as a variable x, so 0.95=0.95x/(0.95x+0.05(1-x)). Solving for x, we find that x=0.5, meaning that 50% of the population would need to have Covid for a test with 95% accuracy to indicate a 95% likelihood of having Covid.